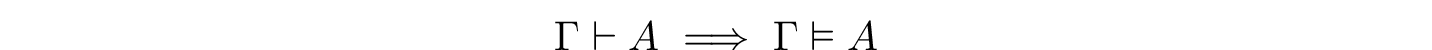
Apr 12, 2020 Tags: philosophy
This post is at least a year old.
This post has been on my roster for a long time; I’ve finally decided to write it after talking to my partner about their intuitions for symbolic logic.
Developing intuitions for soundness and completeness took me a long time, and first required me to develop intuitions for syntax and semantics.
My intuition for syntax in the context of formal languages revolves around rules and productions. The rules of a formal language comprise that language’s grammar; sentences that are instantiations of those rules are valid productions in the language.
For example, a minimal language with just one base case:
And one inductive rule:
Has infinitely many (syntactically) unique productions:
AAAA…and so on.
Where syntax is about rules and productions, semantics is about values and evaluation.
Intuitions around syntactic structure lead the way to an immediate semantic intuition: that
multiple syntactically unique productions (e.g. A and ¬¬A) can have the same
semantic value (in this case, both A) when evaluated.
My intuition around evaluation is (probably) a common one: evaluation amounts to assigning every atom in the sentence a value and determining the truth-functional value of the overall sentence. A complete truth table is an easy way to visualize every possible evaluation of a sentence:
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Here is the stodgy statement of soundness that was passed down to me:
Expressed in English: “if Γ syntactically entails A, then Γ semantically entails A.”
Where Γ is a set of sentences in the language serving as the hypotheses for A.
Broken down:
A if there exists a formal proof of A from Γ.
A if A can be proved from all of Γ
using the formal inference rules of the logic in question.A if and only if all evaluations in which all of Γ hold
are also evaluations in which A is true.
A if and only if there doesn’t exist a
countermodel of the union of Γ and {A}.It took me a long time to understand (1) what this even meant (beyond understanding the formal definition), and (2) why it wasn’t trivially true for all logics.
My intuition: a language is sound if and only if I can take any valid set of productions as
premises (Γ) and one production as a conclusion (A) such that A is provable from Γ
and evaluate those productions such that every true evaluation across all of Γ is
also a true evaluation of A.
This is easy to visualize as a relationship between purely syntactic operations on a proof (here in Fitch form) and its corresponding truth table:
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
A is derivable from Γ; all lines where all evaluations of Γ are true are also
lines where evaluations of A is true (specifically, just line 1).
With an intuition for soundness, completeness is straightforward:
With a similar English expression: “if Γ semantically entails A, then Γ syntactically entails A.”
The intuition here is just the converse of the above: a language is complete if and only if I can take any full expansion
of evaluations (i.e., expanded truth table) for A from Γ and demonstrate a corresponding syntactic form
where A is provable from Γ.
We can demonstrate this using the expansion of evaluations from the truth table above:
Despite my best efforts, my intuitions above are dense (in both lingo and structure) and difficult to communicate. Here’s my attempt to reduce them even further:
In other words: if I know that a language is sound, then I know that I can take an arbitrary proof in it and expect a fully expanded set of possible evaluations from it.
If I know that a language is complete, then I know that, given an fully expanded set of possible evaluations, I can reconstruct the original proof.
If I know both, then I know that every fully expanded set of evaluations corresponds to a proof, and every proof corresponds to a set of evaluations.
Where φ is metasyntactic notation for “any atom (i.e., a, b, c, …) or previous sentence” ↩