
Mar 9, 2020 Tags: cryptography, devblog, programming, rust, security
This post is at least a year old.
Tl;DR: I went ahead and wrote a pure-Rust implementation of Skipjack this past weekend. You can find it on GitHub as skipjack.rs and on Cargo as skipjack.
Skipjack (or SKIPJACK) is a block cipher, best known for its use in the NSA’s Clipper chip. It was officially declassified in 1998, although its design appears to have begun in the late 1980s and was stabilized by 19931.
There’s a decent amount of technical and historical information about Skipjack online already, but here are the interesting bits:
ABAB pattern: 8 rounds
of rule “A” are applied, then 8 of “B”, and so on.I had the following goals for my Rust implementation:
It turned out that #1 was relatively easy — despite a decent amount of technical documentation on Skipjack’s design, actual implementations appear to be relatively scarce. After finishing, the primary ones appear to be an “optimized” version in C originally by Panu Rissanen in 1998 (here’s one copy, but many variants are available online) and a few toy and educational implementations. This old NIST document lists validated implementations, but nothing that’s likely to be readily available online.
To accomplish #2, I needed a specification of Skipjack that I could understand and follow. Fortunately, NIST provides one in their “Skipjack and KEA Algorithm Specifications” from 1998. The linked PDF was created from scans, making it annoying to copy the F-table from — someone was kind enough to transcribe it back into text here.
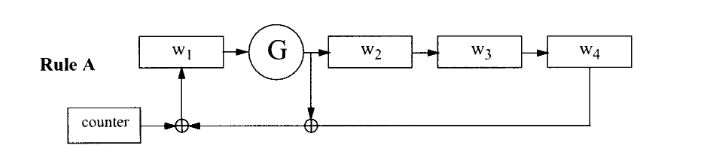
Skipjack’s structure is remarkably simple: there are two main rules (A and B), each
of which applies the permutation rule G. G in turn integrates bytes from the secret key
(“cryptovariable” in NIST’s terminology) via a lookup into F, which is a fixed 1-1
table on Page 8 of the specification. Each rule also integrates the current counter
(which begins at 1 when encrypting, and at 32 when decrypting) as it mixes the input block.
The rules for A and B (and A' and B', for decryption) are specified as:

NIST provides a key for all of this syntax, but in essence: each rule operates on the individual
“words” of the input block, where each word is 16 bits. Each superscript indicates
the “step number”, indicating that step k + 1 takes the values produced by k as its inputs.
With rule A as an example:
w1) becomes the result of rule G on the w1 produced
by the last step, XOR’ed with the last step’s w4 and counterw2 becomes the result of rule G on the last round’s w1w3 becomes the last round’s w2w4 becomes the last round’s w3And as Rust:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
fn rule_a(words: &mut [u16; 4], counter: &mut u16, key: &[u8; 10]) {
// Make a copy of our input block (as words) so that we don't accidentally
// use the words that we're modifying while performing the rule.
let original_words = words.to_owned();
// Word 1 becomes an application of the G rule on itself,
// XOR'ed with Word 4 and the current counter.
// Observe that we pass `counter - 1` to rule G; G takes the
// current step number, which is always the counter minus 1.
words[0] = rule_g(original_words[0], *counter - 1, key) ^ original_words[3] ^ *counter;
// Word 2 becomes an application of the G rule on Word 1.
words[1] = rule_g(original_words[0], *counter - 1, key);
// Word 3 becomes Word 2.
words[2] = original_words[1];
// Word 4 becomes Word 3.
words[3] = original_words[2];
// We're done with this round, so increment the counter.
*counter += 1;
}
The specification also provides each rule in a schematic format, although I personally find them a little harder to interpret:
The permutation rule G is also relatively straightforward. It operates on a single word,
subdividing into bytes g1 and g2, which eventually become
g5 and g6 via a four-round Feistel structure:
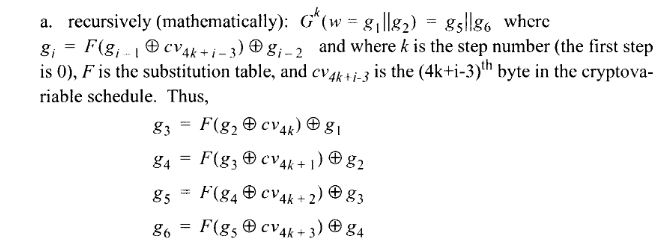
In other words:
g3 becomes the XOR of g1 and a byte of table F, where
the index into F is determined by the XOR of g2 and the 4kth byte of the
secret key (mod 10, since the key is only 10 bytes), where k is the step number.
…and similarly for g4 and onwards. This has the effect of mixing each sub-round
of G into the next, along with 4 bytes of secret key.
as Rust, again:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
fn rule_g(word: u16, step: u16, key: &[u8; 10]) -> u16 {
let bytes = word_to_bytes(word);
let (g1, g2) = (bytes[0], bytes[1]);
// Round 1: Transform g2 and a byte of the secret key into an index into F,
// then XOR with g1.
let g3 = F[(g2 ^ key[((4 * step) % 10) as usize]) as usize] ^ g1;
// Round 2: Transform g3 and a byte of the secret key into an index into F,
// then XOR with g2.
let g4 = F[(g3 ^ key[(((4 * step) + 1) % 10) as usize]) as usize] ^ g2;
// Round 3: Transform g4 and a byte of the secret key into an index into F,
// then XOR with g3.
let g5 = F[(g4 ^ key[(((4 * step) + 2) % 10) as usize]) as usize] ^ g3;
// Round 4: Transform g5 and a byte of the secret key into an index into F,
// then XOR with g4.
let g6 = F[(g5 ^ key[(((4 * step) + 3) % 10) as usize]) as usize] ^ g4;
// The result of rule G is the combination of the bytes from
// the final two rounds into a single word.
bytes_to_word([g5, g6])
}
(Both rule_g and rule_a are copied directly from skipjack.rs’s source. You can also find
rule_b and the inverse rules in it!)
The schematics for G and G' are a little more obvious, thanks to the linear re-integration
of each previous round’s output:
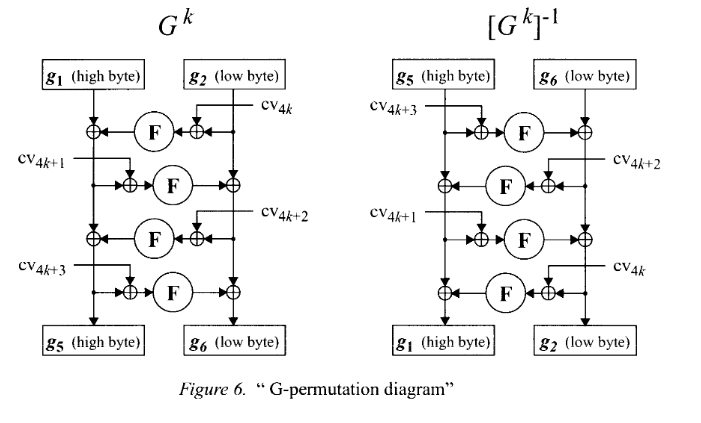
All told, skipjack.rs is only 375 lines of Rust, including all comments
and unit tests. With comments and test lines removed, the actual Skipjack implementation
becomes just 165 lines. That could further be reduced by replacing the 64 literal
calls to rule_a, rule_a_inv, &c with trivially inlinable loops, e.g.:
1
2
3
for _ in 0..8 {
rula_a(&mut words, &mut counter, &key);
}
…but we’re not playing code golf here.
All told, Skipjack took me about 8 hours to implement. That’s a lot less time than I expected, given that:
Implementing Skipjack was a nice reminder that the concepts behind block ciphers are not especially difficult, and can be easily implemented with a little bit of tolerance for jargon. It was also a nice reminder of how treacherous that feeling of ease can be in cryptographic contexts — my understanding of the why of Skipjack’s internals is still superficial3, and my choice of language (vs. C/C++) is probably the only thing keeping my implementation from being full of subtle cross-platform bugs.
In the same vein as above: I’ve been writing C for about a decade, and have felt “comfortable” doing bitwise operations (meaning that I can do them without reference) for about 7 years. “Comfortable” is in scare-quotes there because doing bitmath in Rust feels like a totally different beast — I don’t have the background anxieties that I carry from C, and I trust that my operations will perform consistently across different platforms, word sizes &c.
Before writing skipjack.rs, my intuition around straight-line code had been that it was a constraint, something that I’d have to consciously aspire to in a context where I’d want or need it.
It was surprising, then, to realize that I had written my Skipjack implementation with absolutely no loops or branches from the very beginning and without intending to. This makes perfect sense in retrospect (Skipjack itself has a fixed number of rounds, and the rest is just mathematical operations and lookups), but it wasn’t an intuition I had before.
From this 1993 report. ↩
Biham et al. found an attack on Skipjack when reduced to 16 rounds within a day of declassification. This was subsequently extended to 31 rounds, but with an only-slightly-faster-than-exhaustive result. ↩
Case in point: I have absolutely no idea what would happen were I to transpose two values in the F-table. ↩